感染症の数理モデルは完全に間違っていた

最近では「何もしなければ42万人死ぬ」の西浦先生を真に受ける人も少なくなりました。西浦先生は1月5日のNHKでこういっています。記事になったのが1/5なのでおそらく取材は1/4とか1/3でしょう。

東京の感染者数シミュレーション十分に減少させるには

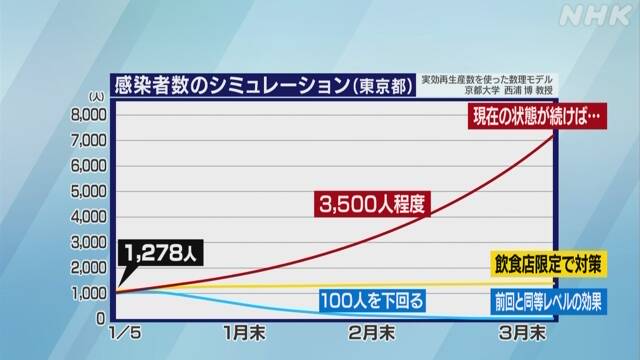
現在の感染状況から、東京都の実効再生産数はおよそ1.1となり、仮に新たな対策をせずにこの状態が続くとすると2月末時点での新たな感染者数は1日およそ3500人、3月末にはおよそ7000人まで増えるとみられるということです。

3月末には東京の感染者数は7000人どころかその20分の１ですし、そもそも

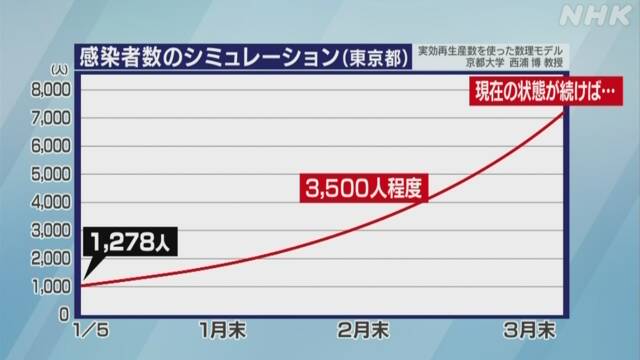
こんなにはまったくならずに、それどころか取材を受けた1/4には発症ベースでピークアウトしまして

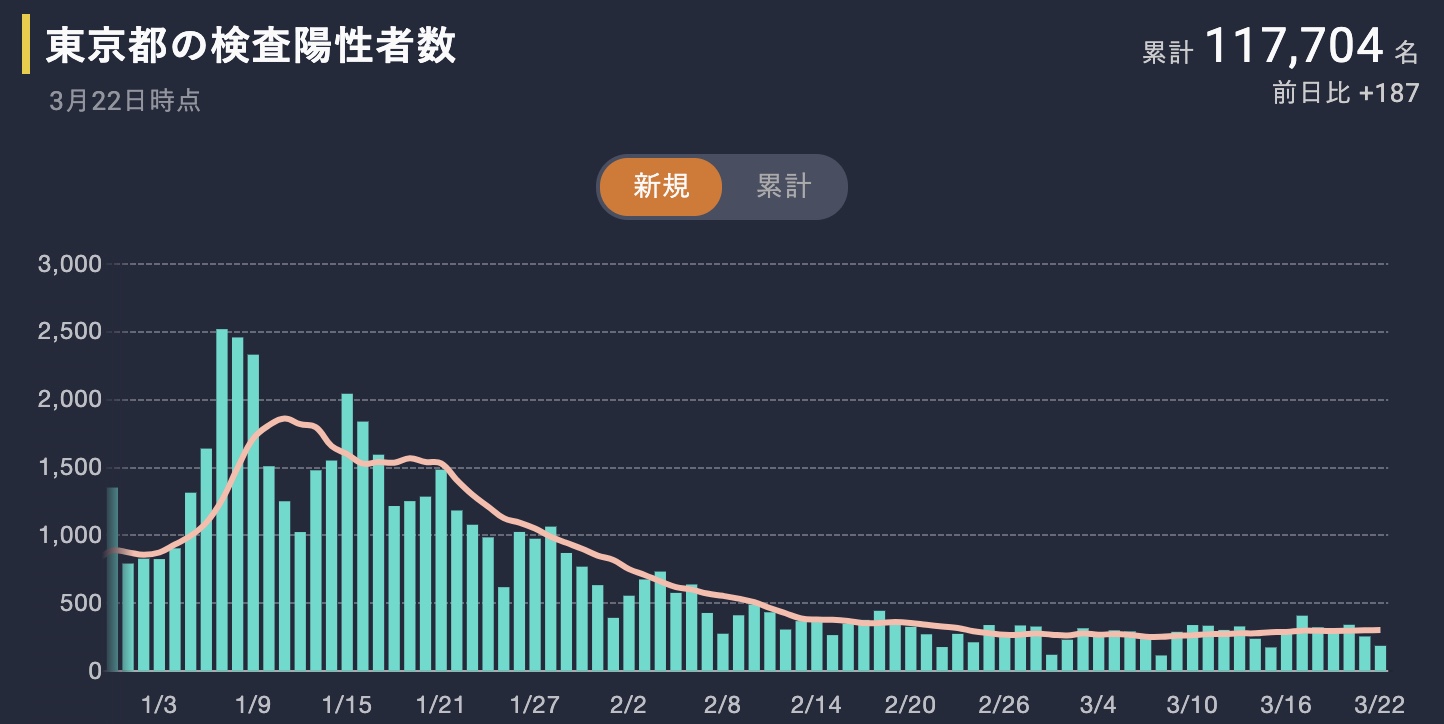
こうなりました。

医クラの中には「西浦先生は何もしない場合42万人死ぬ」を「なにもしないという前提を付けていた」といってかばう人もまだいますが、1/5のケースではそんなことはいっていません。

新たな対策をしないと

と仰いましたが、新たな対策といっても1/7からの緊急事態宣言ですが、その前の1/4にこのようにピークアウトしているので「あらたな対策をしなくても」ピークアウトして感染は急激に収束したわけです。ここで、

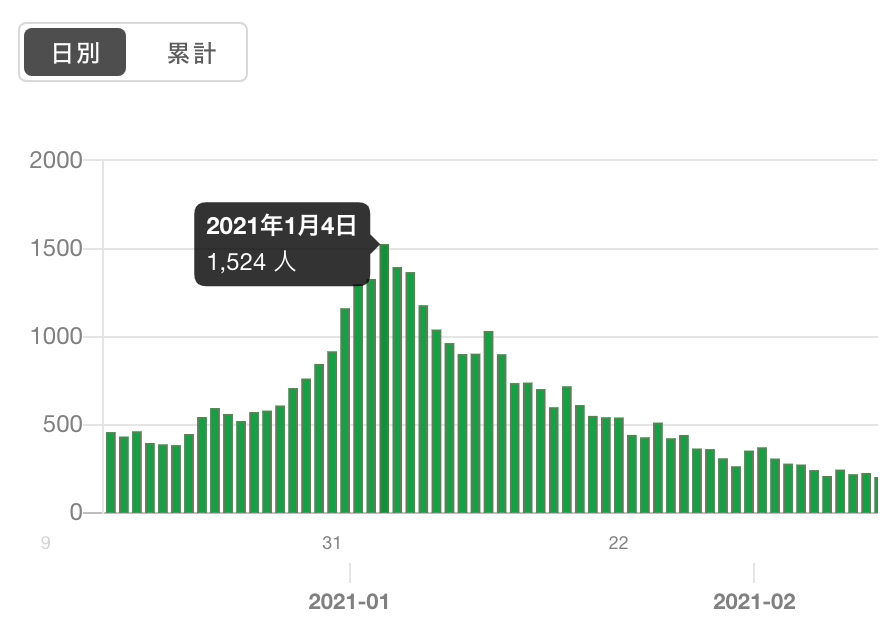
西浦先生の数理モデルは完全に間違っていたと証明済み

というのは火を見るより明らかだろうと思います。それでも地球は回っていると言う方はお申し出ください。

ほかにも、数理モデルを使って予測した大学関係の皆さんは全員が全員お外しになりました。コロナについては従来の数理モデルは役に立たなかったのは明白。これはどうしてか。ここからはわたしの仮説でして従来の感染学の専門家は全否定すると思いますが、これ以外に外れた理由とどうすれば修正できるかを提案できる方はぜひ教えてください。

kokoroyuki/iStock

現在の数理モデルがコロナに通用しない永江仮説

以前書いたエントリーです。

外れまくりの西浦先生のシミュレーションをバッチリ当たるようにする秘策

世の中にはこれでも理解できない人がいるので、イラストを作ったのでそれで説明します。

まず、世界各国の死者数の違いは、デブ率も多少は影響しますが致死率はそれほど変わらないのです。少なくとも何十倍も違いません。

通算の死者数/感染者数、つまり致死率は２月に計算したら

アメリカ　1.7%
イギリス　2.8%
フランス　2.4%
イタリア　3.4%

日本　1.5%
韓国　1.8%
フィリピン　2.0%
ベトナム　1.8%
タイ 0.37%

です。死者数が何十倍も違うのは感染する比率の問題です。人口100万人あたりの感染者数は

アメリカ　92165
イギリス　63208
フランス　65971
イタリア　56619

日本　3627
韓国　1946
フィリピン　6185
マレーシア　10311
シンガポール　10238
で

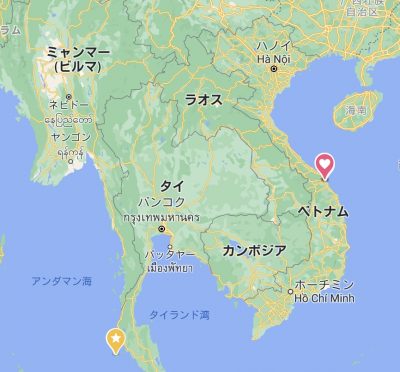
ベトナム　26
タイ 405
ラオス　7
カンボジア 108

と、感染率の低い東アジアの中でもインドシナ半島諸国が異様に感染率が低いことが分かります。去年２月にベトナムに行ったときも炸裂中の韓国やイタリアからたくさんの観光客風来ていたがコレ。カンボジアも３月までゆるゆるで欧米人がたくさんいたそうだ。

人口比率で見ると、総人口のうち感染した人の割合は

欧米　5~10%
東アジア 日本が0.4% ~　マレーシア1%
東アジアの中のインドシナ半島　ほとんどゼロ~0.04% ということになります。日本でコロナに罹患したのは200人に１人です。

どうしてこんなに罹患率に差が出るのか。これがファクターXですが、別に理由は研究者に任せますが、わたしはこういうことだと仮説を立てました。
コロナにはすべての人が均等にかかりやすいわけではなく、

自己免疫でかかりやすい人とかかりにくい人がいる

ということ。イラストにするとこうなります。

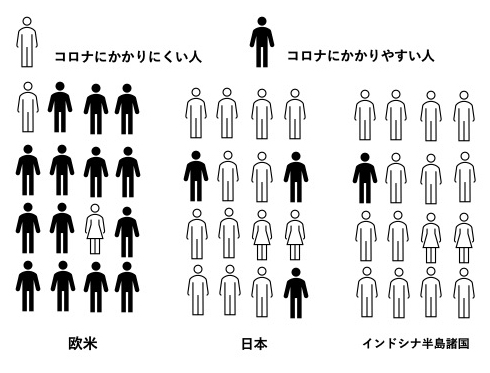
欧米ではコロナに罹患するしきい値の低い人が大多数のため、この黒い人たちの間で指数関数的に感染が拡大します。それでも人口の10%程度ですのでそこまで罹患するといったんは収束し、抗体が切れる４~6ヶ月後くらいにまた波が来ます。例えばニューヨーク。

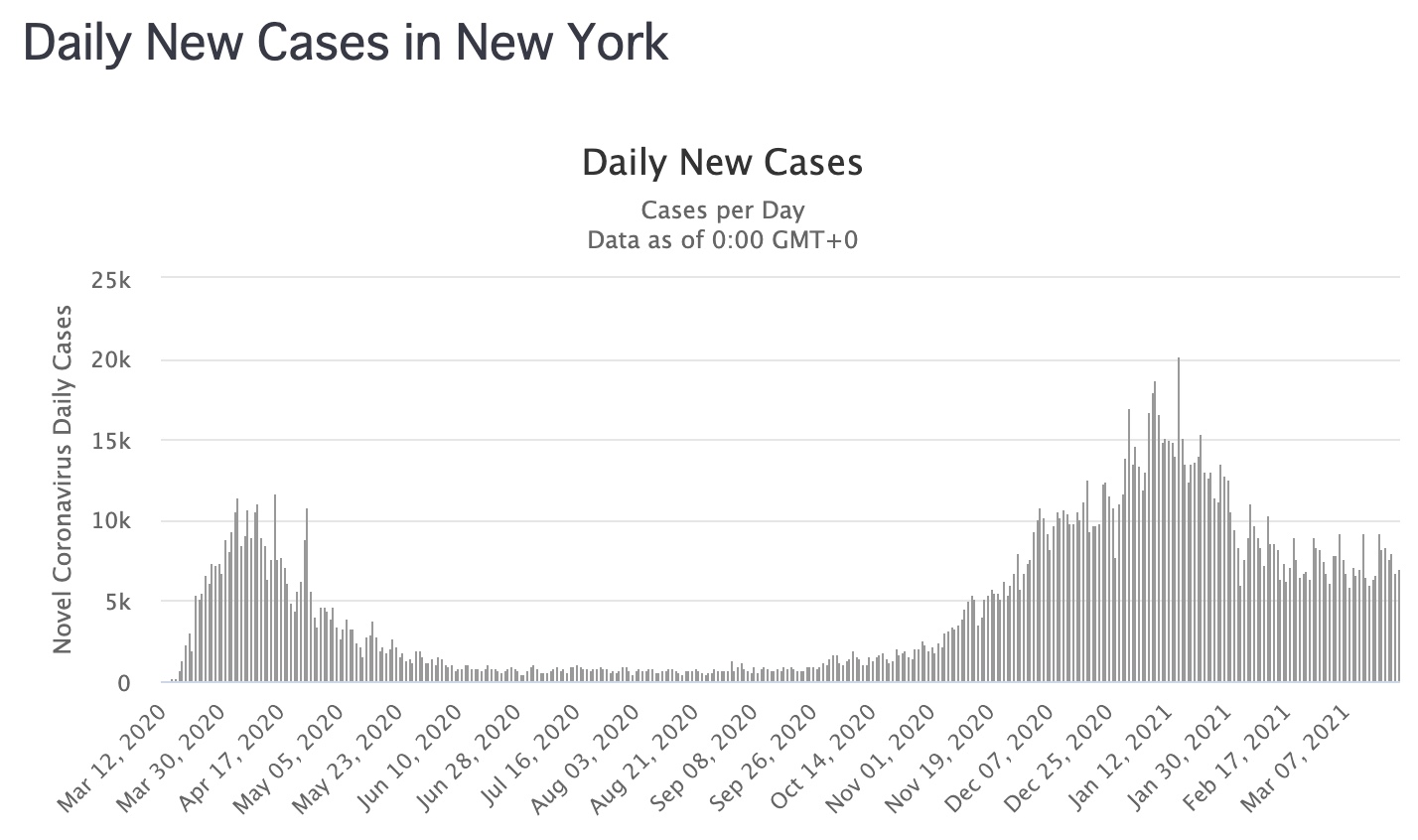
しかし日本では罹患しやすい黒い人たちが少ないのでなかなか指数関数的には拡大しません。そしてすぐに収束します。

わかりましたね。いままでの古い数理モデルでは、全員が罹患する確率は同じで全員が黒だったのです。だから人口の全員がかかるまで指数関数的に感染は拡大するはずだった。ココが間違っていたのです。

考えて見ればインフルエンザだって毎年国民の1000万人しか罹患しなかった。

インフルエンザワクチンには感染予防効果はほとんどないので全員にかからないとおかしいわけだが、ワクチンを打っていなくてもかかったことかせない人はたくさんいる。つまり国民の1%くらいがかかりやすい人たちだったのです。そして各人のしきい値は寝不足だったり太陽を浴びてなかったり、基礎疾患があったりで変動する。寝不足の医療従事者は罹患しやすいわけ。

しかし、高齢者施設や病院ではどうかというと、入居している人たちは基礎疾患かあり高齢で抵抗力も弱いから

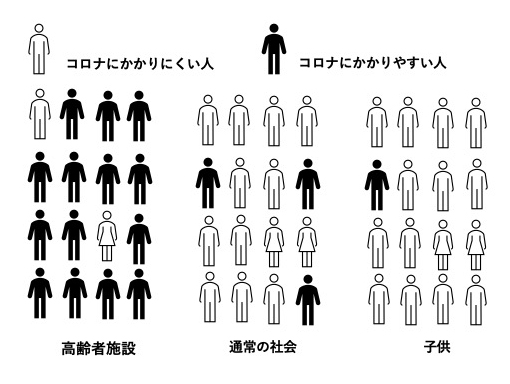
こういう感じなのだと思う。だから院内感染や施設内感染があるとその施設では数理モデルで指数関数的に感染が広がり何百人もの感染者を出す。逆に子供がかかりにくいのは、その群の中にしきい値が低い個体が少ないのです。

ここまでが私の仮説です。

どうすれば数理モデルが的中するようになるか

簡単です。

数理モデルの前提にもうひとつの関数をくわえる。つまり、「かかりやすい人の濃度」です。日本の場合１年で0.4%しか罹患しなかったので、たとえば人口の0.2%が罹患したら収束するように設定する。ちなみに12月〜１月10日までの陽性者の総数は23万人なので日本の人口の0.2%でした。いま自分で書きながら電卓叩いて鳥肌立ったわ。w

この関数を0.05~0.4%くらいに何種類も想定して第１波、第２波、第３波に当てはめれば次の第４波は数理モデルで的中するはずです。おそらく温暖な季節は自己免疫が高いのでこの関数は低くなり、寒くなる時期は高くなる。素人に言われて腹が立つかもしれませんが、研究者の方は一度試してみてください。別にたいした手間でもないでしょ。

くりかえすがいままでの数理モデルは「国民全員が罹患する」という前提が間違っていたのです。

別に誰が言っていたっていいじゃん。他に説明が付くのであれば誰か1/4にピークアウトして一気に陽性が減った理由を説明してください。

編集部より：この記事は永江一石氏のブログ「More Access,More Fun!」2021年3月24日の記事より転載させていただきました。